
Nauki ścisłe przyswajamy odmiennie niż wiele innych – bardziej uchwytnych i codziennych umiejętności. Początki są długie i trudne, za to później następuje gwałtowny postęp – mamy więc do czynienia z „efektem kuli śniegowej”. Zrozumienie tego zjawiska pozwala nam przewidywać przebieg edukacji i dobrać optymalne metody nauczania.
Dynamika nauki
Dynamika przyswajania umiejętności zależy od rodzaju zdolności, której się uczymy. Spróbujmy prześledzić trzy różne sposoby uczenia się na trzech prostych przykładach. Pierwszy, to umiejętność powtarzalna, szybko schodząca do podświadomości – jazda samochodem. Drugą jest umiejętność typowo pamięciowa – nauka historii ograniczająca się w naszym przykładzie do zapamiętywania dat, nazwisk, wydarzeń, miejsc etc. Trzecia, to umiejętność złożona, wymagająca świadomego myślenia przy pomocy abstrakcyjnych pojęć – matematyka.
Chciałbym jeszcze zaznaczyć, że poniższa dyskusja nie artykułem naukowym. Jej cel jest dydaktyczny – chodzi o unaocznienie pewnych ogólnych zależności. Opieram się w niej zarówno na danych naukowych jak i rozległym doświadczeniu – swoim oraz innych nauczycieli.
Umiejętność powtarzalna
Krzywa nauki dla jazdy samochodem będzie prezentować się z grubsza jak na poniższym rysunku. 100% oznacza jakiś arbitralny poziom umiejętności, który chcielibyśmy nabyć. Co charakteryzuje naszą krzywą? Można zauważyć, że najpierw dość szybko rośnie (co ilustruje szybkie uczenie się), a następnie postęp zaczyna spowalniać. Proszę zwrócić uwagę, że połowę zakładanego poziomu umiejętności osiągamy wcześniej niż w połowie poświęconego na całą naukę czasu.

Faktycznie – analizując proces nauki jazdy samochodem możemy zauważyć, że zrazu jest on bardzo intensywny. Jednak po ok. 30 godzinach młody kierowca może już sam całkiem bezpiecznie poruszać się po drodze. Kolejne dziesiątki godzin samodzielnej jazdy powodują wzrost jego umiejętności, ale nie tak szybki, jak te pierwsze kilka-kilkanaście godzin. Wtedy zauważalny postęp następował wręcz z godziny na godzinę.
Przykłady innych czynności o podobnej krzywej nauki, to np. sprawność pisania na komputerowej klawiaturze lub szybkiego i sprawnego przyrządzania sushi.
Umiejętność pamięciowa
Nieco inaczej sprawa będzie się miała dla nauki historii – umiejętności pamięciowej. W tym przypadku postęp jest w przybliżeniu liniowy, co ilustruje poniższy wykres. Znaczy to, że umiejętności (naszej wiedzy) przybywa proporcjonalnie do poświęcanego czasu – przez cały okres nauki. Gdybyśmy rozłożyli materiał powiedzmy na 10 podobnych części, możemy spodziewać się, że nauka każdej z nic zajmie nam podobną ilość czasu. Połowę zakładanej wiedzy osiągamy po połowie potrzebnego czasu etc.

Tę krzywą nauki najłatwiej jest sobie wyobrazić – jest chyba najbardziej intuicyjna. To podobne do nalewania wody do dużego wiadra. Woda nalewa się w takim samym tempie cały czas. Podobnie – lepienie pierogów. Jeśli w godzinę ulepimy 50 pierogów, to w 2h ulepimy 100, w 3h – 150 itd.
Krzywa nauki dla umiejętności złożonych
Wreszcie mamy krzywą nauki matematyki. Proszę zwrócić uwagę, że przebiega ona odwrotnie do pierwszej – czerwonej krzywej. Nauka z początku jest powolna, a postęp niewielki w stosunku do poświęcanego czasu. Połowę zakładanego postępu umiejętności osiągamy znacznie później, niż w pozostałych dwóch przypadkach. Jednak, w miarę upływu czasu tempo nauki wzrasta. Czasami mówi się na to: „efekt kuli śniegowej”.

W podobny sposób kumuluje się zysk z inwestycji (gdy zarobione procenty inwestujemy dalej). W taki sposób zachowuje się też lawina. Małe z początku obsunięcie śniegu, ciągnąc za sobą ten, który napotka na drodze, kończy się oberwaniem całego stoku górskiego.
Porównajmy jeszcze dla porządku wszystkie trzy krzywe na jednym rysunku. Proszę zwrócić uwagę, jak różne jest tempo przyrastania umiejętności w początkowym okresie nauki (czerwona krzywa rośnie szybko, a zielona powoli). Ta sytuacja dramatycznie odwraca się jednak pod koniec. Czerwona krzywa się wypłaszcza – postęp na niej jest coraz mniejszy. Za to zielona gwałtownie pnie się ku górze.

Właśnie ten ostatni – szybki etap wzrostu zielonej krzywej wiąże się z tzw. efektem kumulacji wiedzy – a potoczenie efektem kuli śniegowej. W następnych sekcjach opowiem skąd się on właściwie bierze i jakie konsekwencje wynikają z niego dla ucznia, nauczyciela i metod nauki.
Przyczyny kumulacji
Jak już widzieliśmy nie wszystkie typy umiejętności podlegają prawu kumulacji. Czemu podlegają jej nauki ścisłe? W ich przypadku rozumienie zagadnień bardziej zaawansowanych zawsze opiera się na konieczności bardzo dobrego przyswojenia zagadnień prostszych. Bardzo dobrego, a nie powierzchownego czy przeciętnego. Przykład: nauka rachunku różniczkowego nie jest możliwa bez dobrego opanowania materiału z zakresu funkcji matematycznych. Inny przykład: nie sposób posługiwać się potęgami i pierwiastkami nie pojąwszy uprzednio zasad mnożenia i dzielenia.
Dlatego wszelkie niedostatki w podstawach niezmiennie prześladują uczniów na wyższych etapach edukacji. Są one najczęstszą przyczyną frustracji, zwątpienia w siebie i niechęci do przedmiotu. Szczególna trudność nauki przedmiotów ścisłych wynika z ich samej natury, jest niejako w nie wbudowana. Nie jest niczym dobrym ani złym – jest faktem naturalnym dla tych dziedzin wiedzy. Z tego powodu jednak konieczne jest uczenie się ich w sposób bardziej przemyślany.

Wpływ na przebieg nauki
Nietrudno więc zrozumieć, że nauka zagadnień bardziej zaawansowanych bez ugruntowania tych prostszych jest skazana na niepowodzenie. To tak, jakby chcieć wystartować samolotem, któremu brakuje jednego skrzydła. Albo zbudować wieżowiec bez fundamentu i dwóch pierwszych pięter. Lub instalować ogrzewacz do ciepłej wody w domu, do którego w ogóle nie ma doprowadzonego wodociągu.
Dlatego zielona krzywa jest na początku bardziej płaska od pozostałych. Niezbędne jest założenie solidnego fundamentu zrozumienia podstaw. Ma to trudną konsekwencję: nauka nie daje szybkich widocznych rezultatów i przez to bardzo łatwo zniechęca. Potęguje odczuwaną presję, która dodatkowo utrudnia proces nauki. (Więcej o wpływie emocji na uczenie się można dowiedzieć się z artykułu Relacja z uczniem.)
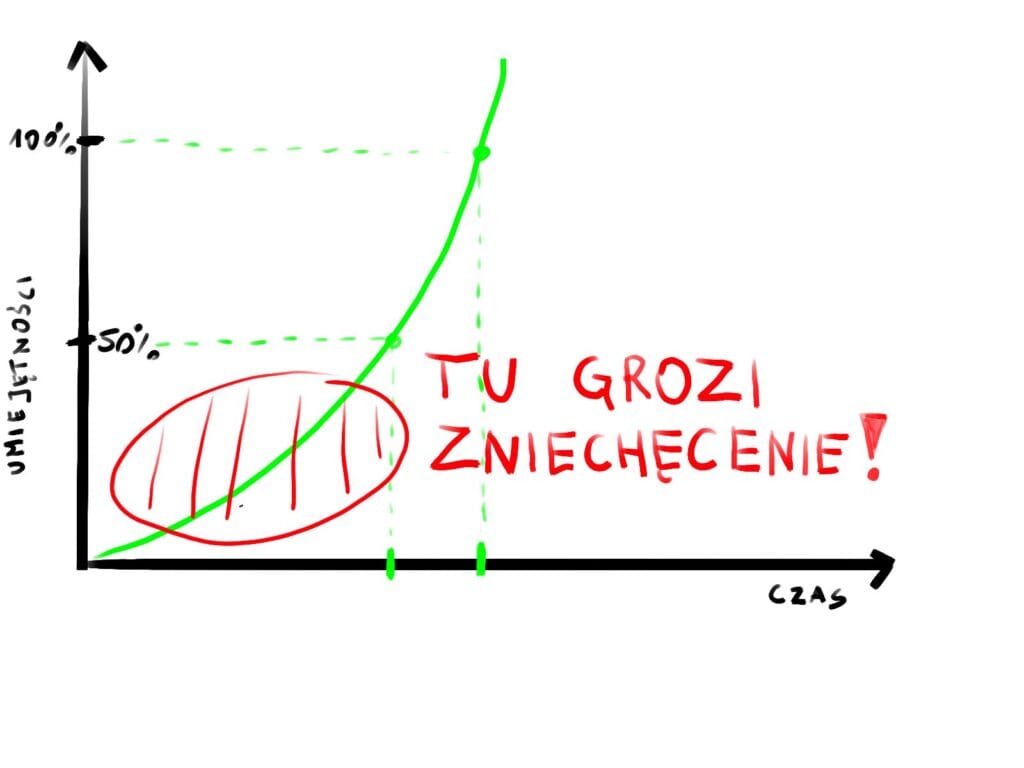
Zatrzymanie się na początkowym etapie przyswajania wiedzy ma jednak fatalne konsekwencje – uniemożliwia poznawanie przedmiotu w następnych latach. Jedna kluczowa, a nie utrwalona umiejętność potrafi upośledzić całą dalszą naukę. Koronnym przykładem, z którym często się spotykam, jest nieumiejętność rachowania ułamków. Nierzadko przygotowanie maturzysty zaczynam od ponownej nauki tego tematu, normalnie opanowywanego najpóźniej w 7 klasie szkoły podstawowej.
Systemowe błędy
Innym, klasycznym, przykładem niezrozumienia natury nauki matematyki jest podejście wielu szkolnych nauczycieli. Polega ono na tym, że ucząc się nowego działu (np. ciągów) mało czasu poświęca się na proste ćwiczenia z zupełnie podstawowego zakresu: czym jest ciąg, jak oznaczamy poszczególne wyrazy ciągu, a jak ogólny jego wzór etc. Skoro są to wiadomości podstawowe, wydają się proste. A skoro są proste, poświęca się na nie minimum czasu, żeby móc dalej pędzić z materiałem.
Konsekwencją jest dezorientacja u uczniów i bałagan w ich głowach. Mały problem z rozumieniu oznaczeń za chwile będzie prowadził do kompletnej katastrofy przy bardziej złożonych zadaniach. Niedostateczna uwaga poświęcona ułożeniu i sprawdzeniu wiedzy zupełnie podstawowej, stawia bariery – niekiedy trudne do przekroczenia – w dalszej nauce. W konsekwencji zaś nakręca spiralę: próba – porażka – frustracja – zniechęcenie.
Odczuwam wręcz pewien wstyd, że zwracam uwagę na tak oczywiste rzeczy. Prawdą jest jednak, że brak wspomnianego fundamentu jest niezawinioną przez wielu uczniów zmorą ich szkolnej czy uniwersyteckiej codzienności. Uniemożliwia im on wędrówkę w górę po zielonej krzywej. Przez to nawet, pomimo ciągłego wysiłku, cały czas widzą co najwyżej mizerne efekty. Jeśli mimo wszystko postępują, to wolno i bardzo nierównomiernie.

Część pedagogów próbuje zaradzić tej sytuacji poprzez rytualne zadawanie ogromnych ilości zadań domowych. To oczywiście także nie pomaga (o czym więcej w artykule Trening sportowy). Przypomina raczej jakiś mroczny pogański kult, w którym w ofierze składane są kolejne godziny z życia uczniów, ich rozum, poczucie wartości i sen. Wszystko w nadziei, że kapryśny bożek matematyki wleje im w końcu magicznym sposobem upragnioną wiedzę do głowy. Jest to głupie i okrutne jednocześnie.

Jak uczyć, aby nauczyć?
Na szczęście nikt nie jest skazany na tkwienie w podobnej ciemności i ciemnocie. Z rozumnego namysłu wypływają następujące wnioski praktyczne, które stosujemy w codziennej pracy z uczniami.
Po pierwsze – zakładamy solidny fundament wiedzy. Zalepiamy dziury z przeszłości, a w przypadku nowych zagadnień upewniamy się na różne sposoby co do poprawnego zrozumienia kluczowych pojęć i logicznych zależności. Nie pozwalamy uczniom, choćby chcieli, prześlizgnąć się nad nimi bez zrozumienia.
Po drugie – w tym delikatnym czasie zdejmujemy z uczniów presję i szczególnie dbamy o ich motywację. Po to, by nie zniechęcili się do pracy, zanim nie ujrzą jej pierwszych wyraźnych i trwałych efektów.
Po trzecie – proponujemy takie zadania – zarówno na lekcji jak i w domu – które rozwijają myślenie i zrozumienie zagadnień. Nie ilość, a jakość samych zadań i ich rozwiązywania decyduje o szybkości postępu.

Po czwarte – gdy uczeń szczęśliwie dojdzie do rejonu kumulacji, mobilizujemy go do zwiększonego wysiłku, by uczynił jak największe postępy. Najczęściej jednak wtedy nie potrzebuje on specjalnie naszej motywacji.
Kula śniegowa już pędzi sama.
Pan Stanisław


